| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- hashing
- Eulerian circuit
- graph
- mathematics
- 백준
- BST
- DynamicProgramming
- Dag
- flows
- graph modeling
- Euler circuit
- BFSDFS
- BOJ
- GCD
- POJ
- dynamic programming
- disjoint-set
- scc
- Eulerian path
- Algospot
- CS Academy
- Greedy
- Cycle detecting
- Euler path
- Shortest path
- Segment Tree
- backtracking
- implementation
- Sieve_of_Eratosthenes
- bitmask
- Today
- Total
그냥 하는 노트와 메모장
트리 유사도 분석 - 특징 벡터 추출 본문
[개요]
웹 동적 분석을 진행하는데 분석 시간 이슈가 상당히 많다. 검출할 수 있는 취약점이 많으면 많을수록 그 취약점을 검출하기 위해 시간이 걸리기에 결과적으로 분석 시간이 늘어나게 되는데, 이를 줄이기 위해서 생각한 것이 바로 DOM 유사도 분석이다. DOM 유사도 분석을 통해 비슷한 페이지나 이미 분석이 끝난 부분을 분석에서 제외하여 시간을 줄이자는 게 내 아이디어. 개인적으로 연구를 진행했다.
이 포스팅은 특징 벡터 추출하는데에 집중하며, 이 특징 벡터를 어떻게 굽고 삶느냐에 따라 유사도가 바뀐다. 따라서 이러한 설정은 각자 개인이 판단하시길..

[사전에 고려된 구조]
1. 단순 특징 비교
각 서브 트리에서 특징별로 노드를 나열하여 단순 비교한다. 가령 DOM의 경우 태그 이름별로 각 트리에 몇 번 등장했는지로 비교한다. 이 방식은 트리의 구조를 전혀 고려하지 않기 때문에 이 특징 벡터로는 유사도 알고리즘을 설계하기가 굉장히 어렵다.
2. 텍스트 diff 알고리즘 활용
DOM은 태그별로 노드가 구분된다. 따라서 주어진 DOM에 대한 HTML 소스 코드를 얻을 수 있고, 여기서 두 개의 HTML 소스 코드에 대해 indentation을 같게줘서 통일된 구조로 텍스트 diff를 진행할 수 있다. 간단하게 말하면 git처럼 두 소스코드를 비교하여 어느정도 다른지를 특징 벡터로 두는 것이다. 하지만 이 방식은 텍스트 비교라서 트리 구조를 전혀 따지지 않는다. 어느 텍스트가 같더라도 그 루트 노드에서 그 노드까지의 경로가 같다는 보장이 없다.
[내가 생각한 구조]
1. Randomized Longest Common Branch Sequences
1. 각 트리에서 리프노드 하나씩 u, v를 고른다.
2. u에서 루트까지의 최단 경로를 노드로 표현한걸 path-u라고 하자. path-u와 path-v는 일차원으로 표현되는데 이 때 연속으로 공통된 경로의 최대 길이를 찾는다.
- 알고리즘
path-u의 길이를 Lu, path-v의 길이를 Lv라고 하면 O(Lu * Lv)의 시간복잡도를 가지는 다이나믹 프로그래밍을 작성한다.
현재 방문하고 있는 노드가 각각 a, b라면 아래 세 가지 경우에 대해 처리한다.
1. a를 최대 공통 부분에서 제외한다.
2. b를 최대 공통 부분에서 제외한다.
3. a와 b가 특성이 같은 경우 최대 공통 부분에 추가한다.
이를 코드로 작성하며 아래와 같다.
int rec(final Path u, final Path v, int a, int b){
if(a == u.length() || b == v.length())
return 0;
if(dp[a][b] != -1) return dp[a][b];
// case 1), case 2)
dp[a][b] = Math.max(rec(u, v, a+1, b), rec(u, v, a, b+1));
// case 3)
if(tree1[a].equals(tree2[b]))
dp[a][b] = Math.max(dp[a][b], rec(u, v, a+1,b+1));
return dp[a][b];
}3. 1., 2. 과정을 k번 수행해서 가장 많이 겹치는 노드를 기준으로 아래 서브 트리를 분석에서 제외한다.
[분석]
개발자가 소스 코드를 자유롭게 작성할 수 있기 때문에 DOM을 분석할 때 항상 최악의 경우를 생각한다. 따라서 N개의 노드에 대해
- 높이는 O(N)
- 리프 노드의 수는 O(N)
- 다이나믹 프로그래밍 알고리즘 O(Lu * Lv)
- 리프 노드 고를 확률 1/(리프 노드의 수) = 1/N
- 한 번 수행하는데 정확도 F = (실제 최대 공통 서브트리에서 u를 뽑을 확률) * (실제 최대 공통 서브트리에서 v를 뽑을 확률)
실제 최대 공통 서브트리에서 u를 뽑을 확률은 (실제 최대 공통 서브트리에 속한 리프 노드 수) / (전체 리프 노드 수)와 같다. 따라서 실제 최대 공통 서브트리에 속한 리프 노드가 많으면 많을수록 정확도는 올라간다.
- 한 번의 시도가 낮은 정확도를 가지고 있으므로 여러 번 시도해서 정확도를 올린다. 정확도를 올리는 방법은 반대로 에러율을 내리면되므로 한 번 시도에 대한 에러율(E)을 다시 계산하면, E = 1-F가 된다. 따라서 시도 회수를 K라고 정하면 결과에 대한 정확도는 1-E^K이 된다.
[결과]
- 장점: 빠르다. 대다수의 DOM에 대해 테스팅을 진행해본 결과 빠르게 결과를 뽑아낼 수 있었다.
- 단점: 정확도가 낮다. 아무래도 리프 노드에 의존적이기에 DOM 구조 전체를 볼 수 없다. 따라서 이 알고리즘을 쓰더라도 추가적으로 다른 알고리즘을 또 사용해야 구조를 파악할 수 있어보인다.
2. Network flow - MCMF(Minimum Cost Maximum Flow)
MCMF 알고리즘을 사용하여 구현한 이 구조에서 입력으로 두 트리를 넣는다면 결과로 두 트리에서 하나씩 대표 노드를 정해주고 그 노드들로부터 아래 서브트리가 최대로 유사하다는 것을 알 수 있다.
이 방식은 서브 트리 유사도를 매우 세세하게 잡아준다. 먼저 트리 자식 배치 순서가 상관이 없다. 가능한 매칭에 대해 모든 경우를 따지기 때문에 형제 노드간 섞인 것은 무시하여 유사도를 얻을 수 있다.
1. 노드 u, v를 각 트리에서 하나씩 고른다. 단 두 노드의 특성은 반드시 같아야한다(여기서 특성은 사용자가 정의한 특성을 말한다. 가령 DOM의 경우 특성 중 하나를 태그 이름으로 둘 수 있다).
2. u의 자식 노드 중 하나를 x, v의 자식 노드 중 하나를 y라고 하자. 다시금 x와 y를 같다고 판별했을 때 결과값으로 나오는 서브트리 유사도를 x에서 y로 가는 간선의 가중치로 둔다. 모든 경우에 대해 수행하면 그 결과로 이분 그래프가 나온다.
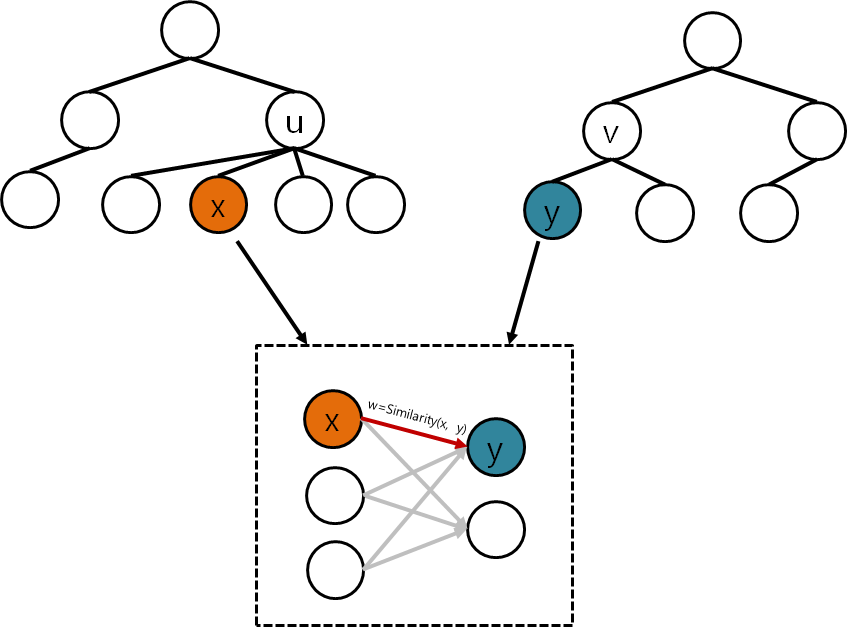
3. MCMF 알고리즘으로 트리 유사도를 도출한다. MCMF를 자바로 구현하면 아래처럼 구현할 수 있다.
// ford-fulkerson using SPFA
private double mcmf(int S, int T, List<List<Edge>> adj) {
double cost = 0;
int i;
while (true) {
for(i = 0; i <= T; i++) {
distance.set(i, 1.0);
parentIndex.set(i, -1);
}
distance.set(S, 0.0);
queue.push(S);
while (!queue.isEmpty()) { // SPFA
int u = queue.poll();
hasQueue.set(u, false);
for (Edge e : adj.get(u)) {
if (e.residualCapacity() > 0 && Math.ceil(distance.get(e.v) * ADJUST_DOUBLE_VALUE) > Math.ceil((distance.get(u) + e.cost) * ADJUST_DOUBLE_VALUE)) {
distance.set(e.v, distance.get(u) + e.cost);
parentIndex.set(e.v, u);
path.set(e.v, e);
if (!hasQueue.get(e.v)) {
hasQueue.set(e.v, true);
queue.push(e.v);
}
}
}
}
if (parentIndex.get(T) == -1) break;
for (i = T; i != S; i = parentIndex.get(i)) {
cost += path.get(i).cost;
path.get(i).addFlow(1, adj);
}
}
return -cost;
}4. MCMF로 얻은 결과는 어느 노드 u, v 기준으로 서브트리를 비교했을 때 얻는 단일값으로 "얼마나" 비슷한지를 [0, 1] 사이 수로 표현하게 특징 벡터 형태로 가공한다.
[분석]
- MCMF 알고리즘 시간 복잡도 O(EF) -> 플로우의 수는 최대의 경우 모든 노드가 매칭이 됐다면 서브 트리의 수와 같게 된다. 따라서 F=N. E는 간선으로 자식들 간의 모든 경우를 매칭해보고 결과를 보기 때문에 E=N^2이 된다. 따라서 MCMF 자체의 시간 복잡도는 O(N^3). 하지만 한 노드에 자식이 몰렸을 경우는 거의 없으므로 일반적으로 O(N^3)보다 시간은 적게 걸린다.
[결과]
- 장점: 확실히 성능은 좋다. 자식들간 뒤엉킨 관계에서도 옳게 매칭하여 최대 공통 서브 트리를 가져올 수 있다.
- 단점: 시간이 너무 오래 걸린다. 자식 수가 많으면 많을수록 비례해서 증가하기 때문에 자연스럽게 오래 걸린다.
※ 참고로 MCMF로 트리 유사도 측정하는걸 문제로 만든 사람이 있다. 심지어 온라인에서 제출할 수 있다.. 문제 및 제출은 http://poj.org/problem?id=2483 에서 하면 된다.
'Research' 카테고리의 다른 글
| 트라이(Trie)와 자바 패키지 (0) | 2021.05.20 |
|---|

