| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Sieve_of_Eratosthenes
- Greedy
- Eulerian path
- implementation
- POJ
- graph modeling
- BFSDFS
- BST
- graph
- Algospot
- GCD
- CS Academy
- 백준
- Eulerian circuit
- Dag
- Shortest path
- hashing
- backtracking
- dynamic programming
- flows
- Euler path
- Cycle detecting
- DynamicProgramming
- Euler circuit
- Segment Tree
- disjoint-set
- scc
- bitmask
- BOJ
- mathematics
- Today
- Total
그냥 하는 노트와 메모장
BOJ 9015 정사각형 본문
BOJ 9015 정사각형
[분류 - 기하, 해싱]
[풀이 - 정답]
주어진 좌표의 수는 N개이고 사각형을 만들기 위해서 O(N^4)이 먼저 떠오르지만 시간초과를 면치못하니 보다 효율적인 구현이 필요하다. 정사각형을 만들기 위해서 일단 임의의 두 점을 잡고 다른 두 점을 찾는 방식을 생각해보자. 이 때 임의의 두 점이 이루는 선분은 사각형의 한 변이 되는데, 이러면 만들 수 있는 사각형은 반드시 두 개다. 한 방향만 선택하여 보도록하자.
일단 임의의 두 점을 선택하자. 이 과정은 O(N^2)이다.
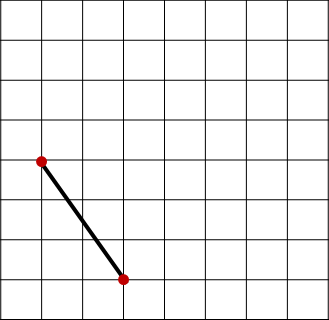
이 두 점이 이루는 선분은 만들고자하는 정사각형의 한 변이 된다.
이 두 점을 포함하는 가장 작은 직사각형을 만들면 아래처럼 빨간 영역의 직사각형을 만들 수 있다.

이 빨간색 영역을 90도씩 회전하면 영역 내에 있는 대각선들 역시 모두 90도를 이루고, 이 대각선들을 잇는다면 그것이 곧 정사각형이 된다.

따라서 찾고자 하는 두 점 역시 정수 좌표이고 그건 아래 그림에서 보라색 두 점임을 알 수 있다. 기존 빨간색 영역을 이루는 직사각형 크기를 구하고 이를 이용해서 파란색, 주황색 영역을 이용하여 보라색 두 점을 구할 수 있다.

보라색 두 점을 찾을 때, 데이터 셋과 제한 시간이 다소 빡빡하기 때문에 적절한 해싱이 필요하다. 나는 unordered_set을 사용했다.
#include<cstdio>
#include<unordered_set>
#include<algorithm>
using namespace std;
const int MAX_N = 3e3, OFFSET = 1e4, OS = 2e4+1;
struct _p { int x, y; }p[MAX_N];
bool operator<(const _p& a, const _p& b) { return a.x != b.x ? a.x < b.x : a.y < b.y; }
bool operator==(const _p& a, const _p& b) { return a.x == b.x && a.y == b.y; }
int main() {
int tc, N, i, j, ans, dy, dx, area, np1, np2;
unordered_set<int> pos;
scanf("%d", &tc);
while (tc--) {
pos.clear();
ans = 0;
scanf("%d", &N);
for (i = 0; i < N; i++) {
scanf("%d%d", &p[i].x, &p[i].y);
p[i].x += OFFSET, p[i].y += OFFSET;
pos.insert(p[i].x * OS + p[i].y);
}
for (i = 0; i < N; i++) for (j = i + 1; j < N; j++) {
_p& p1 = p[i], & p2 = p[j];
dx = p2.x - p1.x, dy = p2.y - p1.y;
area = dx * dx + dy * dy;
if (area < ans || p1.y - dx < 0 || p2.y - dx < 0) continue;
np1 = (p1.x + dy) * OS + p1.y - dx;
np2 = (p2.x + dy) * OS + p2.y - dx;
if (pos.find(np1) != pos.end() && pos.find(np2) != pos.end())
ans = area;
}
printf("%d\n", ans);
}
return 0;
}
[풀이 - WA(실수(double) 오차)]
사실 이 글을 쓴 이유는 이 풀이를 너무 쓰고 싶었다. 수학적을 맞는데 왜맞틀이기 때문이다.
여기서 쓰는 풀이는 그냥 나의 넋두리다. 수학적으론 맞지만 컴퓨터 계산상에선 틀린 풀이다(파이썬으론 맞을 수도 있겠다).
임의의 두 점을 잡는다. 이 때 이 두 점이 이루는 선분은 만들고자 하는 정사각형의 대각선을 이룬다. 이 때 나머지 두 점은 보라색 두점을 이룬다.

두 벡터를 잡자. A=X-p1, B=p2-X로 두자. 그러면 두 가지 성질을 알 수 있다.
1. 길이
당연하게도 정사각형이기 때문에 두 벡터의 크기는 같다. 이 때 일차식으로 표현된다.

2. 내적
두 벡터의 내적의 값은 0이다. 바로 수직인 성질을 이용하는 것이다. 이 때 원으로 표현된다. 다르게 표현하자면 두 점을 지름으로 두는 원을 생각하고, 거기서 지름을 한변으로 두고 호에서 임의의 점을 두면 이 세 점이 이루는 삼각형은 반드시 직각 삼각형이다.

이 두 성질을 이용하여 일차식에서 2차원 원에 대입하고, 계산하면 보라색 두 좌표를 구할 수 있다!

근데 IEEE 754 부동소수점 표기법의 특유 오차 범위로 인해 WA를 받았는데, 적절하게 정수 좌표 존재로 변환하지 못해 결국 포기했다 ㅠ
#include<iostream>
#include<set>
#include<cmath>
#include<algorithm>
#include<cassert>
using namespace std;
const int MAX_N = 3e3;
inline void roundUp(long double& a) {
a = round(a * 1000) / 1000;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int tc, N, i, j, ans;
long double A, B, C, T, K, a, b, c, d, det, x1, x2, y1, y2, area;
pair<int, int> pos[MAX_N];
cin >> tc;
while (tc--) {
ans = 0;
cin >> N;
for (i = 0; i < N; i++)
cin >> pos[i].first >> pos[i].second;
sort(pos, pos + N);
for (i = 0; i < N; i++) for (j = i + 1; j < N; j++) {
/*
1. length
(x-a)^2 + (y-b)^2 = (x-c)^2 + (y-d)^2
-2ax+2cx+a^2+b^2-c^2-d^2 = 2(b-d)y
-> y = (-2ax+2cx+a^2+b^2-c^2-d^2) / (2b - 2d) = Tx + K
2. dot
(x-a, y-b) X (c-x, d-y) = 0
= -x^2 + (a+c)x -ac -y^2 + (b+d)y - bd
= -x^2 + (a+c)x -ac -(T^2x^2+2TKx+K^2) + (b+d)(Tx+K) - bd
= -(1+T^2)x^2 +(a+c+bT+dT-2TK)x -ac -bd + bK + dK - K^2
= Ax^2 + Bx + C
A = -(1+T^2)
B = a + c + bT + dT - 2TK
C = -ac -bd + bK + dK - K^2
*/
a = pos[i].first, b = pos[i].second, c = pos[j].first, d = pos[j].second;
area = ((a - c) * (a - c) + (b - d) * (b - d)) / 2;
if (area < ans || b == d) continue;
T = (c - a) / (b - d);
K = (a * a + b * b - c * c - d * d) / (2 * b - 2 * d);
A = -(1 + T * T);
B = a + c + T * (b + d - 2 * K);
C = -a * c - b * d + K * (b + d - K);
det = B * B - 4 * A * C; // 무조건 2개의 해를 가지게 되어 있음 det > 0
x1 = (-B + sqrt(det)) / (2 * A);
x2 = (-B - sqrt(det)) / (2 * A);
y1 = T * x1 + K;
y2 = T * x2 + K;
roundUp(x1); roundUp(y1);
roundUp(x2); roundUp(y2);
auto it = lower_bound(pos, pos + N, make_pair((int)x1, (int)y1)) - pos;
auto jt = lower_bound(pos, pos + N, make_pair((int)x2, (int)y2)) - pos;
if (it != N && jt != N && pos[it].first == x1 && pos[it].second == y1 && pos[jt].first == x2 && pos[jt].second == y2)
ans = max((long double)ans, ((a - c) * (a - c) + (b - d) * (b - d)) / 2);
}
cout << ans << '\n';
}
return 0;
}'Solved problems' 카테고리의 다른 글
| BOJ 10538 빅 피처 (0) | 2020.12.11 |
|---|---|
| BOJ 2638 - 치즈 (0) | 2020.11.13 |
| BOJ 1053 - 팰린드롬 공장 (0) | 2020.11.13 |
| BOJ 2618 - 경찰차 (0) | 2020.11.13 |
| BOJ 1600 - 말이 되고픈 원숭이 (0) | 2020.11.13 |
